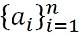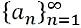Unterschied zwischen Sequenz und Serie
Share
In Mathematik und Statistik ist die Linie, die Sequenz und Reihen abgrenzt, dünn und unscharf, weshalb viele denken, dass diese Begriffe dasselbe sind. Dennoch unterscheidet sich der Begriff der Sequenz von Serien in dem Sinne Sequenz bezieht sich auf eine Anordnung in der bestimmten Reihenfolge, in der verwandte Begriffe aufeinander folgen, d. h. sie weist eine identifizierte erste Einheit, zweite Einheit, dritte Einheit usw. auf.
Wenn eine Sequenz einer bestimmten Regel folgt, wird sie als Progression bezeichnet. Es ist nicht genau das Gleiche wie Serie was als Summe der Elemente einer Sequenz definiert wird. Lesen Sie den Artikel, um den signifikanten Unterschied zwischen Sequenz und Serie zu erfahren.
Inhalt: Sequenz Vs Serie
Vergleichstabelle
| Vergleichsgrundlage | Sequenz | Serie |
|---|---|---|
| Bedeutung | Sequenz wird als Menge von Zahlen oder Objekten beschrieben, die einem bestimmten Muster folgen. | Serie bezieht sich auf die Summe der Elemente der Sequenz. |
| Auftrag | Wichtig | Manchmal wichtig |
| Beispiel | 1, 3, 5, 7, 9, 11… n… | 1 + 3 + 5 + 9 + 11… n… |
Definition der Sequenz
In der Mathematik ist eine geordnete Menge von Objekten oder Zahlen wie a1, ein2, ein3, ein4, ein5, ein6… einn… . Man spricht von einer Sequenz, wenn sie nach bestimmten Regeln einen bestimmten Wert hat. Die Mitglieder der Sequenz werden als Begriff oder Element bezeichnet, das einem beliebigen Wert der natürlichen Zahl entspricht. Jeder Begriff in einer Sequenz bezieht sich auf den vorhergehenden und den nachfolgenden Begriff. Im Allgemeinen weisen Sequenzen versteckte Regeln oder Muster auf, die Ihnen helfen, den Wert des nächsten Begriffs herauszufinden.
Der n-te Term ist die Funktion der ganzen Zahl n (positiv), die als allgemeiner Term der Sequenz angesehen wird. Eine Sequenz kann endlich oder unendlich sein.
- Endliche Sequenz: Eine endliche Folge stoppt am Ende der Liste der Zahlen a1, ein2, ein3, ein4, ein5, ein6… einn, wird vertreten durch:
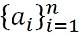
- Unendliche Sequenz: Eine unendliche Sequenz bezieht sich auf eine Sequenz, die endlos ist, a1, ein2, ein3, ein4, ein5, ein6… einn… .., wird vertreten durch:
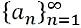
Definition von Serie
Das Hinzufügen der Terme einer Sequenz (an) ist als Serie bekannt. Wie bei Sequenzen können Serien auch endlich oder unendlich sein, wobei eine endliche Serie eine ist, die eine endliche Anzahl von Begriffen hat, die als a geschrieben sind1 + ein2 + ein3 + ein4 + ein5 + ein6 + … einn. Im Gegensatz zu unendlichen Serien, bei denen die Anzahl der Elemente nicht begrenzt ist oder die nicht enden, werden sie als a geschrieben1 + ein2 + ein3 + ein4 + ein5 + ein6 + … einn +… .
Wenn eine1 + ein2 + ein3 + ein4 + ein5 + ein6 + … einn = Sn, dann Sn gilt als Summe von n Elementen der Serie. Die Summe der Begriffe wird häufig durch das griechische Sigma (Ʃ) dargestellt. Daher,
Hauptunterschiede zwischen Sequenz und Serie
Der Unterschied zwischen Sequenz und Serien kann aus folgenden Gründen eindeutig gezogen werden:
- Die Sequenz ist definiert als eine Sammlung von Zahlen oder Objekten, die einem bestimmten Muster folgen. Wenn die Elemente der Sequenz zusammengefügt werden, werden sie als Serie bezeichnet.
- Reihenfolge ist wichtig in einer Reihenfolge, da es eine bestimmte Regel gibt, die das Muster der Reihenfolge vorschreibt. Daher unterscheiden sich 1, 2, 3 und 3 von 3, 1, 2. Andererseits kann in einer Serienreihenfolge die Reihenfolge der Erscheinung eine Rolle spielen oder nicht, wie bei einer absolut konvergenten Serie die Reihenfolge keine Rolle spielt. Also ist 1 + 2 + 3 gleich 3 + 1 + 2, nur ihre Reihenfolge ist unterschiedlich.
Fazit
Arithmetische Progression (A.P.) und Geometric Progression (G.P.) sind ebenfalls Sequenzen und keine Serien. Arithmetische Progression ist eine Sequenz, in der die aufeinander folgenden Ausdrücke wie 2, 4, 6, 8 usw. einen gemeinsamen Unterschied aufweisen. Im Gegensatz dazu ist in einer geometrischen Abfolge jedes Element der Folge das gemeinsame Vielfache des vorangehenden Ausdrucks wie 3, 9, 27, 81 und so weiter. In ähnlicher Weise ist die Fibonacci-Sequenz auch eine der beliebten unendlichen Sequenzen, in der jeder Term durch Addition der zwei vorhergehenden Terme 1, 1, 3, 5, 8, 13, 21 usw. erhalten wird.
