Unterschied zwischen Gleichem und Äquivalent
 Share
Share
Hauptunterschied - Gleich oder Gleichwertig
Gleich und Äquivalent sind Begriffe, die in der Mathematik häufig verwendet werden. Das Hauptunterschied zwischen gleich und gleichwertig ist der Begriff gleich bezieht sich auf Dinge, die in allen Aspekten ähnlich sind, während der Begriff Äquivalent bezieht sich auf Dinge, die in einem bestimmten Aspekt ähnlich sind. Beachten Sie das in der Mengenlehre, Die Wörter „gleich“ und „gleichwertig“ haben bestimmte Bedeutungen, wie wir weiter unten sehen werden.
Was bedeutet gleich?
Im Allgemeinen sind zwei Dinge gleich, wenn sie in jeder Hinsicht ähnlich sind.
Im Falle der Mengenlehre sind zwei Mengen gleich, wenn beide die gleichen Elemente enthalten. Das Auftrag in denen sie in einem Satz aufgeführt sind, spielt keine Rolle. Nehmen wir zum Beispiel an
 und
und
 dann,
dann,
der Satz  ist gleich dem Satz
ist gleich dem Satz  .
.
Was bedeutet Äquivalent?
Zwei Dinge können als gleichwertig bezeichnet werden, wenn sie unter einer bestimmten Bedingung ähnlich sind. Deshalb, ob zwei Entitäten sind Äquivalent weitgehend hängt davon ab unter der Bedingung, mit der wir ihre Gleichwertigkeit beschreiben. Zum Beispiel sind die Zahlen 2 und 7 in dem Sinne äquivalent, dass sie beide Primzahlen sind. Wenn jedoch die Bedingung, an der wir interessiert sind, herauszufinden ist, ob Zahlen gerade sind, dann sind dies 2 und 7 nicht Äquivalent. Wir benutzen die Symbole  oder
oder  um das anzuzeigen
um das anzuzeigen  und
und  sind gleichwertig.
sind gleichwertig.
Nachdem ein Kriterium definiert wurde, erfüllen die Gleichwertigen die Kriterien Äquivalenzbeziehungen:
- Reflexivität:
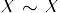
- Symmetrie: Ob
 , dann
, dann 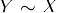
- Durchlässigkeit: Ob
 und
und 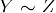 , dann
, dann 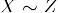
In der Mengenlehre gibt es zwei Mengen Äquivalent wenn sie die gleiche Anzahl von Elementen haben. Die Elemente selbst müssen auch nicht gleich sein, nur Die Anzahl der Elemente muss gleich sein. Nehmen wir zum Beispiel an
 und
und
 dann,
dann,
Die Sätze  und
und  sind gleichwertig.
sind gleichwertig.

Symbole zum Ausdruck von Gleichheit und Gleichwertigkeit
Unterschied zwischen Gleichem und Äquivalent
Allgemeine Bedeutung
Wenn zwei Dinge sind gleich, Sie sind in allen Aspekten ähnlich.
Wenn es so ist Äquivalent, Sie sind in einem bestimmten Aspekt ähnlich.
In der Satztheorie
Wenn zwei Sätze sind gleich, Sie enthalten die gleichen Elemente.
Wenn zwei Sätze sind Äquivalent, sie enthalten das gleiche Anzahl von Elemente.
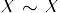
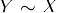
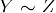 , dann
, dann