Wie berechnet man die Halbwertszeit?
 Share
Share
In diesem Abschnitt werden wir etwas über die Halbwertszeit lernen und die Formel zur Berechnung der Halbwertszeit ableiten. In Radioaktivität, halbes Leben ist die Zeit, die eine Hälfte der radioaktiven Kerne in einer Probe eines radioaktiven Isotops zum Zerfall benötigt. Die Anzahl der radioaktiven Kerne in einer Probe nimmt mit der Zeit exponentiell ab. Zur Berechnung der Halbwertszeit wird daher die Mathematik des exponentiellen Zerfalls verwendet. Die Halbwertszeit ist ein äußerst wichtiges Konzept für die Anwendung von Radioaktivität. Beispielsweise dürfen Radioisotope, die in der Strahlentherapie in Organe eingeführt werden, nicht zu lange im Körper eines Patienten verweilen. Auf der anderen Seite müssen Isotope, die zur Datierung historischer Artefakte verwendet werden, eine lange Halbwertzeit haben, sodass bis heute genug von ihnen geblieben sind, um das Alter der Objekte zu bestimmen.
Unterschied zwischen zufälliger und spontaner Natur des radioaktiven Zerfalls
Radioaktiver Zerfall wird als beides eingestuft zufällig und spontan.
- Radioaktiver Zerfall ist zufällig weil wir nicht bestimmen können, wann ein bestimmter Kern zerfallen wird, oder bestimmen, wie lange es dauern würde, bis ein bestimmter Kern zerfallen würde. Folglich hat jeder radioaktive Kern in einer Probe zu einem gegebenen Zeitpunkt die gleiche Wahrscheinlichkeit für das Abklingen.
- Radioaktiver Zerfall ist spontan weil es nicht von äußeren Bedingungen beeinflusst wird.
Was ist Half Life?
Die Anzahl der radioaktiven Kerne in einer Probe nimmt ab, da der Kern, sobald er durch Alpha-, Beta- und Gammazerfall zerfällt, nicht mehr denselben Zerfallsprozess durchlaufen kann. Die Anzahl der radioaktiven Kerne in der Probe nimmt exponentiell ab.
Das Aktivität, oder der Zerfallsrate,ist die Änderungsrate der Anzahl radioaktiver Kerne. Dies ist gegeben durch,

Das negative Vorzeichen bedeutet, dass die Anzahl der radioaktiven Kerne in einer Probe ist abnehmend im Laufe der Zeit. $ latex \ lambda & s = 1 $ heißt das Zerfall konstant. Es gibt die Wahrscheinlichkeit an, dass ein bestimmter Kern pro Zeiteinheit zerfällt. Die Zerfallskonstante hat einen bestimmten Wert für einen bestimmten nuklearen Zerfallsprozess. Je höher der  , Je höher die Wahrscheinlichkeit des Zerfalls und die Anzahl der radioaktiven Kerne in der Probe nimmt schneller ab.
, Je höher die Wahrscheinlichkeit des Zerfalls und die Anzahl der radioaktiven Kerne in der Probe nimmt schneller ab.
Ist die Anzahl der radioaktiven Kerne in einer Probe gleichzeitig  ist
ist  , dann die Anzahl der radioaktiven Kerne
, dann die Anzahl der radioaktiven Kerne  in der probe nach einer zeit
in der probe nach einer zeit  ist gegeben durch:
ist gegeben durch:

Die Anzahl der radioaktiven Kerne in der Probe nimmt ab exponentiell. Halbes Leben ( ) Ist der Zeitraum, in dem die Anzahl der radioaktiven Kerne in der Zeit halbiert wird. Wenn wir eine Grafik zeichnen, wie sich die Anzahl der radioaktiven Kerne in der Probe mit der Zeit verändert, erhalten wir die folgende Grafik:
) Ist der Zeitraum, in dem die Anzahl der radioaktiven Kerne in der Zeit halbiert wird. Wenn wir eine Grafik zeichnen, wie sich die Anzahl der radioaktiven Kerne in der Probe mit der Zeit verändert, erhalten wir die folgende Grafik:

Berechnung der Halbwertszeit - Kurve des radioaktiven Zerfalls
So berechnen Sie die Aktivität
Die Aktivität der Probe ist proportional zur Anzahl der vorhandenen radioaktiven Kerne. So können wir eine gleichwertige Aussage treffen,

woher  ist die Aktivität der Probe zum Zeitpunkt
ist die Aktivität der Probe zum Zeitpunkt  , mit
, mit  die Tätigkeit wann
die Tätigkeit wann  .
.
Wenn ein Diagramm der Aktivität im Verhältnis zur Zeit gezeichnet wird, wird ein Diagramm mit derselben Form erzeugt (d. H. Die Aktivität fällt auch exponentiell ab)..
Die Aktivität wird mit der SI-Einheit gemessen Becquerel (Bq). Eine Aktivität von 1 Bq entspricht einer Rate von 1 Zerfall pro Sekunde. Das Curie (Ci) ist eine andere Einheit zur Messung der Aktivität. 1 Ci = 3,7 × 1010 Bq.
Halbwertszeit-Formel
Wir werden nun eine Formel herleiten, um die Halbwertszeit von der Zerfallskonstante zu erhalten. Wir fangen mit an,

Nach einer Weile  , die Anzahl der radioaktiven Atomkerne. So,
, die Anzahl der radioaktiven Atomkerne. So,  , oder
, oder

Aus dem natürlichen Logarithmus beider Seiten ergibt sich:

und so,

Wie berechnet man die Halbwertszeit?
Beispiel 1
Indium-112 hat eine Halbwertszeit von 14,4 Minuten. Eine Probe enthält 1,32 × 1024 Atome von Indium-112.
a) Bestimmen Sie die Zerfallskonstante
b) Finden Sie heraus, wie viele Atome von Indium-112 nach 1 Stunde in der Probe verbleiben würden.
a) seit  ,
,

b) Verwenden von  ,
,  Atome.
Atome.
Beispiel 2
Während einer Behandlung von Schilddrüsenkrebs erhält ein Patient eine Probe von Jod-131 zur Einnahme mit einer Aktivität von 1,10 MBq. Die Halbwertszeit von Jod 131 beträgt 8,02 Tage. Bestimmen Sie die Aktivität von Jod-131 im Körper des Patienten nach 5 Tagen Einnahme.
Wir gebrauchen  . Zuerst trainieren wir
. Zuerst trainieren wir  :
:

Dann,
 Mbq.
Mbq.
Hinweis:
- Wir haben den Zerfall pro Tag direkt berechnet und die Halbwertszeit auch in Tagen beibehalten. Also haben die Tage abgesagt, als wir berechneten
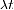 und es war nicht nötig, die Zeiten in Sekunden umzuwandeln (das hätte auch funktioniert, aber es hätte etwas mehr Berechnung nötig)
und es war nicht nötig, die Zeiten in Sekunden umzuwandeln (das hätte auch funktioniert, aber es hätte etwas mehr Berechnung nötig) - In der Realität wäre die Aktivität geringer. Dies liegt daran, dass mit der Aktivität auch eine biologische Halbwertzeit verbunden ist. Dies ist die Rate, mit der der Patient radioaktive Kerne aus seinem Körper ausscheidet.
Beispiel 3
Berechnen Sie die Halbwertszeit eines radioaktiven Isotops, dessen Aktivität in 1000 Jahren um 4% abnimmt.
4% = 0,04. Wir haben nun
 . Ich nehme von beiden Seiten,
. Ich nehme von beiden Seiten,
 pro Jahr.
pro Jahr.
 216 Jahre.
216 Jahre.
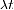 und es war nicht nötig, die Zeiten in Sekunden umzuwandeln (das hätte auch funktioniert, aber es hätte etwas mehr Berechnung nötig)
und es war nicht nötig, die Zeiten in Sekunden umzuwandeln (das hätte auch funktioniert, aber es hätte etwas mehr Berechnung nötig)