Unterschied zwischen Mittelwert und Median
 Share
Share
 Eine zentrale Tendenz impliziert die Tendenz der Datenpunkte, sich um ihren zentralen oder mittleren Wert zu sammeln. Die zwei am häufigsten verwendeten Messgrößen für die zentrale Tendenz sind der Mittelwert und der Medianwert. Bedeuten ist definiert als der "zentrale" Wert der angegebenen Datenmenge, während Median ist der 'mittlere' Wert in dem gegebenen Datensatz.
Eine zentrale Tendenz impliziert die Tendenz der Datenpunkte, sich um ihren zentralen oder mittleren Wert zu sammeln. Die zwei am häufigsten verwendeten Messgrößen für die zentrale Tendenz sind der Mittelwert und der Medianwert. Bedeuten ist definiert als der "zentrale" Wert der angegebenen Datenmenge, während Median ist der 'mittlere' Wert in dem gegebenen Datensatz.
Ein ideales Maß für die zentrale Tendenz ist klar definiert, leicht verständlich und einfach berechenbar. Es sollte auf allen Beobachtungen basieren und am wenigsten von extremen Beobachtungen im Datensatz betroffen sein.
Die Menschen messen diesen beiden Maßen oftmals gegenüber, aber sie sind unterschiedlich. In diesem Artikel werden die grundlegenden Unterschiede zwischen Mittelwert und Mittelwert besonders hervorgehoben. Guck mal.
Inhalt: Mittelwert Vs Median
Vergleichstabelle
| Vergleichsgrundlage | Bedeuten | Median |
|---|---|---|
| Bedeutung | Der Mittelwert bezieht sich auf den einfachen Durchschnitt der angegebenen Werte oder Mengen. | Der Medianwert ist als mittlere Zahl in einer geordneten Liste von Werten definiert. |
| Was ist es? | Es ist ein arithmetischer Durchschnitt. | Es ist ein Positionsmittelwert. |
| Repräsentiert | Schwerpunkt des Datensatzes | Schwerpunkt des Datensatzes Mittelpunkt des Datensatzes |
| Anwendbarkeit | Normalverteilung | Verteilte Verteilung |
| Ausreißer | Mean ist empfindlich gegen Ausreißer. | Der Median ist unempfindlich gegen Ausreißer. |
| Berechnung | Der Mittelwert wird berechnet, indem alle Beobachtungen aufsummiert und der erhaltene Wert durch die Anzahl der Beobachtungen dividiert wird. | Um den Median zu berechnen, wird der Datensatz in aufsteigender oder absteigender Reihenfolge angeordnet. Der Wert, der genau in die Mitte des neuen Datensatzes fällt, ist der Median. |
Definition von Mittelwert
Der Mittelwert ist das weit verbreitete Maß für die zentrale Tendenz, das als Durchschnitt der Wertemenge definiert wird. Es repräsentiert das Modell und den häufigsten Wert des angegebenen Wertebereichs. Es kann sowohl in diskreten als auch in kontinuierlichen Reihen berechnet werden.
Der Mittelwert ist gleich der Summe aller Beobachtungen geteilt durch die Anzahl der Beobachtungen im Datensatz. Wenn der von einer Variablen angenommene Wert gleich ist, ist auch der Mittelwert derselbe. Der Mittelwert kann aus zwei Arten bestehen, dem Stichprobenmittelwert (x̅) und dem Populationsmittelwert (µ). Es kann mit gegebener Formel berechnet werden:
- Arithmetischer Mittelwert:
 wobei Ʃ = griechischer Buchstabe Sigma, bezeichnet "Summe von ..."
wobei Ʃ = griechischer Buchstabe Sigma, bezeichnet "Summe von ..."
n = Anzahl der Werte - Für diskrete Serien:
 wobei f = Frequenz ist
wobei f = Frequenz ist - Für kontinuierliche Servies:
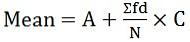 wobei d = (X-A) / C ist
wobei d = (X-A) / C ist
A = angenommener Mittelwert
C = gemeinsamer Divisor
Definition von Median
Der Median ist ein weiteres wichtiges Maß für die zentrale Tendenz und wird verwendet, um den Wert in zwei gleiche Teile aufzuteilen, d. H. Eine größere Hälfte der Stichproben-, Bevölkerungs- oder Wahrscheinlichkeitsverteilung von der unteren Hälfte. Dies ist der mittlere Wert, der erreicht wird, wenn die Beobachtungen in einer bestimmten Reihenfolge (aufsteigend oder absteigend) sortiert werden.
Ordnen Sie für die Berechnung des Medians zuerst die Beobachtungen in der niedrigsten bis höchsten oder höchsten bis niedrigsten Form an, und wenden Sie dann die entsprechende Formel an, da die folgenden Bedingungen erfüllt sind:
- Wenn die Anzahl der Beobachtungen ungerade ist:
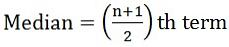 wobei n = Anzahl der Beobachtungen
wobei n = Anzahl der Beobachtungen - Wenn die Anzahl der Beobachtungen ist sogar:
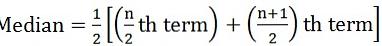
- Für fortlaufende Serien:
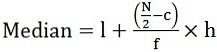 Dabei ist l = untere Grenze der Mittelklasse
Dabei ist l = untere Grenze der Mittelklasse
c = kumulative Häufigkeit der vorhergehenden Mittelklasse
f = Häufigkeit der Mittelklasse
h = Klassenbreite
Hauptunterschiede zwischen Mittelwert und Median
Die signifikanten Unterschiede zwischen Mittelwert und Medianwert sind im folgenden Artikel angegeben:
- In der Statistik wird ein Mittelwert als der einfache Durchschnitt der angegebenen Werte oder Mengen definiert. Der Median soll die mittlere Zahl in einer geordneten Werteliste sein.
- Während der Mittelwert der arithmetische Mittelwert ist, ist der Median der Positionsmittelwert. Im Wesentlichen bestimmt die Position des Datensatzes den Medianwert.
- Der Mittelwert umreißt den Schwerpunkt des Datensatzes, während der Medianwert den mittleren Wert des Datensatzes hervorhebt.
- Der Mittelwert ist für normal verteilte Daten geeignet. Auf der anderen Seite ist der Medianwert am besten, wenn die Datenverteilung schief ist.
- Der Mittelwert wird stark durch den Extremwert beeinflusst, der bei einem Median nicht der Fall ist.
- Der Mittelwert wird berechnet, indem alle Beobachtungen aufsummiert und der erhaltene Wert durch die Anzahl der Beobachtungen dividiert wird. Das Ergebnis ist gemein. Im Gegensatz zum Median ist der Datensatz in aufsteigender oder absteigender Reihenfolge angeordnet. Der Wert, der genau in die Mitte des neuen Datensatzes fällt, ist der Median.
Beispiel
Ermitteln Sie den Mittelwert und den Median des angegebenen Datensatzes:
58, 26, 65, 34, 78, 44, 96
Lösung: Um den Mittelwert zu berechnen, müssen Sie die Summe der Beobachtungen durch die Anzahl der Beobachtungen teilen,

 Mittelwert = 57,28
Mittelwert = 57,28
Um den Medianwert zu berechnen, ordnen Sie zuerst die Reihe in einer Reihenfolge an, d. H. Vom niedrigsten zum höchsten,
26, 34, 44, 58, 65, 78, 96
 wobei n = Anzahl der Beobachtungen
wobei n = Anzahl der Beobachtungen
Fazit
Nach der Überprüfung der obigen Punkte können wir sagen, dass diese beiden mathematischen Konzepte unterschiedlich sind. Das arithmetische Mittel oder der Mittelwert wird als das beste Maß für die zentrale Tendenz angesehen, da es alle Merkmale eines idealen Maßes enthält, es hat jedoch den Nachteil, dass die Abtastschwankungen den Mittelwert beeinflussen.
Ebenso ist der Median eindeutig definiert und leicht zu verstehen und zu berechnen. Das Beste an dieser Maßnahme ist, dass sie nicht von Stichprobenfluktuationen beeinflusst wird. Der einzige Nachteil des Medians besteht jedoch darin, dass er nicht auf allen basiert Beobachtungen. Bei der Einstufung am offenen Ende wird der Median normalerweise dem Mittelwert vorgezogen.
 wobei Ʃ = griechischer Buchstabe Sigma, bezeichnet "Summe von ..."
wobei Ʃ = griechischer Buchstabe Sigma, bezeichnet "Summe von ..." wobei f = Frequenz ist
wobei f = Frequenz ist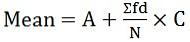 wobei d = (X-A) / C ist
wobei d = (X-A) / C ist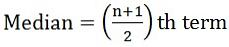 wobei n = Anzahl der Beobachtungen
wobei n = Anzahl der Beobachtungen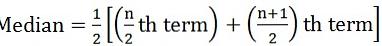
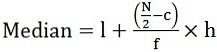 Dabei ist l = untere Grenze der Mittelklasse
Dabei ist l = untere Grenze der Mittelklasse Median = 4th term = 58
Median = 4th term = 58