So finden Sie die Asymptoten einer Hyperbel
 Share
Share
Hyperbel
Die Hyperbel ist eine konische Sektion. Der Begriff Hyperbel bezieht sich auf die beiden getrennten Kurven, die in der Figur gezeigt sind.
Wenn die Hauptachsen mit den kartesischen Achsen übereinstimmen, hat die allgemeine Gleichung der Hyperbel die Form:

Diese Hyperbeln sind um die y-Achse symmetrisch und werden als y-Achsen-Hyperbel bezeichnet. Die Hyperbelsymmetrie um die x-Achse (oder die x-Achsen-Hyperbel) ist durch die Gleichung gegeben,
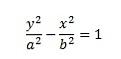 So finden Sie die Asymptoten einer Hyperbel
So finden Sie die Asymptoten einer Hyperbel
Um die Asymptoten einer Hyperbel zu finden, verwenden Sie eine einfache Manipulation der Parabelgleichung.
ich. Zuerst bringen Sie die Gleichung der Parabel auf die oben angegebene Form
Wenn die Parabel als gegeben ist mx2+ny2=l, durch Definieren
ein= √ (l/m) und b= √ (-l/n) woher l<0
(Dieser Schritt ist nicht erforderlich, wenn die Gleichung in Standard von gegeben wird.

ii. Ersetzen Sie dann die rechte Seite der Gleichung durch Null.

iii. Faktorisieren Sie die Gleichung und nehmen Sie Lösungen

Daher sind die Lösungen ,

Gleichungen der Asymptoten sind

Gleichungen der Asymptoten für die x-Achsen-Hyperbel können auch durch dasselbe Verfahren erhalten werden.
Finden Sie die Asymptoten einer Hyperbel - Beispiel 1
Betrachten Sie die durch Gleichung x gegebene Hyperbel2/ 4-y2/ 9 = 1. Finden Sie die Gleichungen der Asymptoten.

Schreibe die Gleichung um und folge dem obigen Verfahren.
x2/ 4-y2/ 9 = x2/ 22 -y2/32 = 1
Durch Ersetzen der rechten Seite durch Null wird die Gleichung zu x2/ 22 -y2/32 = 0.
Faktorisierung und Lösung der Gleichung ergeben,
(x / 2-y / 3) (x / 2 + y / 3) = 0
Gleichungen der Asymptoten sind,
3x-2y = 0 und 3x + 2y = 0
Finden Sie die Asymptoten einer Hyperbel - Beispiel 2
- Die Gleichung einer Parabel wird als -4x² + y² = 4 angegeben

Diese Hyperbel ist eine x-Achsen-Hyperbel.
Umordnung der Begriffe der Hyperbel in den Standard aus gibt
-4x2+ y2= 4 => y2/ 22 -x2/ 12 = 1
Die Faktorisierung der Gleichung liefert folgendes
(y / 2-x) (y / 2 + x) = 0
Daher sind die Lösungen y-2x = 0 und y + 2x = 0.
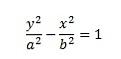 So finden Sie die Asymptoten einer Hyperbel
So finden Sie die Asymptoten einer Hyperbel 